-
-
方差是实际值与期望值之差平方的平均值,而标准差是方差算术平方根。方差是各个数据与平均数之差的平方的和的平均数。
方差的公式
方差是实际值与期望值之差平方的平均值,而标准差是方差算术平方根。在实际计算中,我们用以下公式计算方差。
方差是各个数据与平均数之差的平方的和的平均数,即
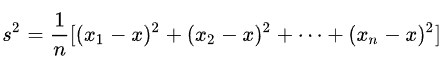
其中,x表示样本的平均数,n表示样本的数量,x1表示个体,而s2就表示方差。
方差和标准差的不同
1、概念不同
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数;
标准差是总体各单位标准值与其平均数离差平方的算术平均数的平方根;
2、计算方法不同
方差的计算公式为:

式中的s2表示方差,x1、x2、x3、.....、xn表示样本中的各个数据,M表示样本平均数
标准差=方差的算术平方根=s=sqrt(((x1-x)2+(x2-x)2+.....(xn-x)2)/n)。
常见方差公式
(1)设c是常数,则D(c)=0。
(2)设X是随机变量,c是常数,则有D(cX)=(c2)D(x)。
(3)设x与Y是两个随机变量,则
D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特别的,当x,Y是两个相互独立的随机变量,上式中右边第三项为0(常见协方差),则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。
(4)D(X)=0的充分必要条件是x以概率为1取常数值c,即P{X=c}=1,其中E(X)=c。
(5)D(aX+bY)=a2DX+b2DY+2abE{[x-E(X)][Y-E(Y)]}。