-
-
注意事项:
1、答卷前，考生务必将自己的姓名，准考证号填写在答题卡上.
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应答案的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回.
一、选择题:本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1.设集合M={1,3,5,7,9}. N={x|2x >7}，则M∩N=
A.{7,9}
B.{5,7,9)
C.{3,5,7,9}
D.{1,3,5,7,9}
2.为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图:
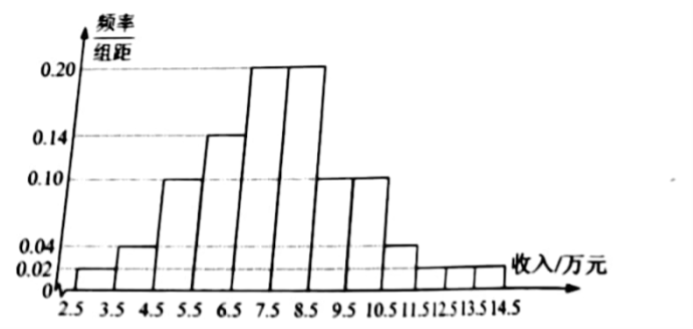
根据此频率分布直方图，下面结论中不正确的是
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间
3．已知(1-i)2z =3+2i，则z =
A. -1-
i
B. -1+i
C. -+i
D. --i
4．下列函数中是增函数的为
A.f(x)= -x
B.f(x)= 
C.f(x)=x2
D.f(x)= 
5．点(3,0)到双曲线
=1的一条渐近线的距离为
A.
B.
C.
D.
6.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量。通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录法的数据V满足
。已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为
A. 1.5 B. 1.2 C. 0.8 D. 0.6
7.在一个正方体中，过顶点A的三条棱的中点分别为E, F, G，该正方体截去三棱锥A-EFG后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是
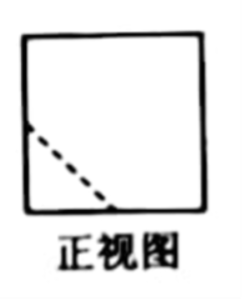
A. 
B. 
C.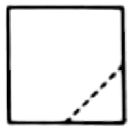 
D.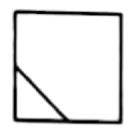 
8.在∆ABC中，已知
则
A. 1 B. 
C. 
D. 3
9.记
为等比数列
的前n项和。若
，则
A. 7 B. 8 C. 9 D. 10
10.将3个1和2个0随机排成一行，则2个0不相邻的概率为
A. 0.3 B. 0.5 C. 0.6 D. 0.8
11、若
∈(0,
),
=
,则
=
A.
B.
C.
D.
12.设f(x)是定义域为R的奇函数，且f(1+x)=f(-x).若f(-
)=
,则f(
)=
A.-
B.- C. D.
二、填空题：本题共4小题，每小题5分，共20分。
13.若向量a,b满足
=3,
=5,a·b=1,则
=________.
14.已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为________.
15.已知函数f(x)=2
的部分图像如图所示，则f(
)=____________.
16.已知
为椭圆C: 
的两个焦点，P，Q为C上关于坐标原点对称的两点，且
=
，则四边形P
Q
的面积为_________.
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤、第17~21题为必考题，每个试题考生都必须作答。第 22、23题为选考题，考生根据要求作答。
(一)必考题:共60分。
17.(12 分)
甲、乙两台机床生产同种产品产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品产品的质量情况统计如下表:
| 一级品 | 二级品 | 合计 |
甲机床 | 150 | 50 | 200 |
乙机床 | 120 | 80 | 200 |
合计 | 270 | 130 | 400 |
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握为机品质量与乙机床的产品质量有差异?
附:
,
|
| 0.010 | 0.001 |
|
|
|
|
18.(12 分)
记,为数列的前n项和，已知
,>0，
,，且数列{
}是等差数列，证明:是等差数列.
19.(12分)
已知直三棱柱ABC-
中,侧面,A
B为正方形,AB=BC=2,E,F分别为AC和C
的中点，BF⊥，
(1)求三棱锥F-EBC的体积:
(2)已知D为棱上的点，证明: BF⊥DE.
20.（12分）
设函数f(x)=
，其中a>0。
（1）讨论f(x)的单调性；
（2）若y=f(x)的图像与x轴没有公共点，求a的取值范围。
21.（12分）
抛物线C的顶点为坐标原点O，焦点在x轴上，直线l:x=1交C于P，Q两点，且OP⊥OQ，已知点M(2,0)，且⊙M与l相切。
（1）求C，⊙M的方程；
（2）设A1，A2，A3是C上的三个点，直线A1A2，A2A3均与⊙M相切，判断直线A2A3与⊙M的位置关系，并说明理由。
（二）选考题：共10分，请考生在22、23题中任选一题作答如果多做，则按所做的第一题计分。
22.[选修4-4：坐标系与参数方程]（10分）
在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=
。
（1）将C的极坐标方程化为直角坐标方程；
（2）设点A的直角坐标为(1,0)，M为C上的动点，点P满足
=
，写出P的轨迹C1的参数方程，并判断C与C1是否有公共点。
23. [选修4-5：不等式选讲]（10分）
已知函数f(x)=|x-2|，g(x)=|2x+3|-|2x-1|。
（1）画出y=f(x)和y=g(x)的图像；
（2）若f(x+a)≥g(x)，求a的取值范围。
文章来源:http://www.gaosan.com/