-
-
反三角函数的导数公式推导过程是利用dy/dx=1/(dx/dy),然后进行相应的换元。反三角函数是一种基本初等函数,它包括反正弦函数、反余弦函数、反正切函数以及反余切函数的求导。

反函数求导方法
若F(X),G(X)互为反函数,
则:F'(X)*G'(X)=1
E.G.:y=arcsinx x=siny
y'*x'=1 (arcsinx)'*(siny)'=1
y'=1/(siny)'=1/(cosy)=1/根号(1-sin^2y)=1/根号(1-x^2)
其余依此类推。
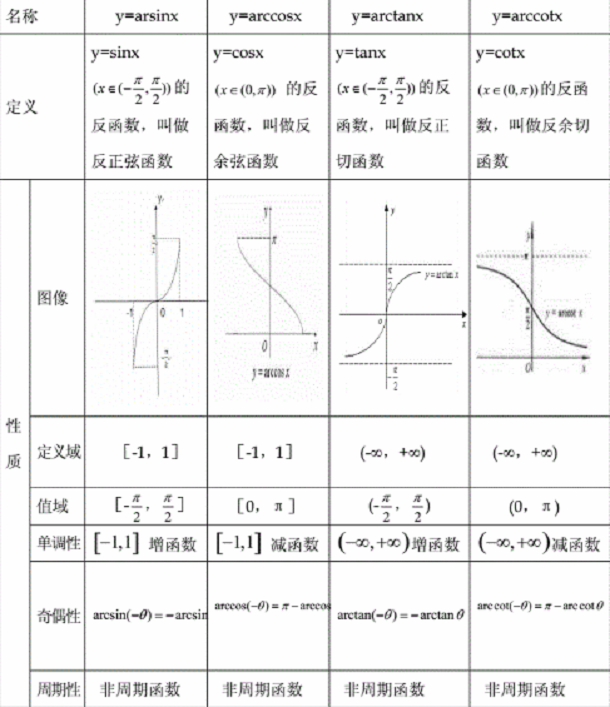
反三角函数
反三角函数是一种基本初等函数。它是反正弦arcsinx,反余弦arccosx,反正切arctanx,反余切arccotx,反正割arcsecx,反余割arccscx这些函数的统称,各自表示其反正弦、反余弦、反正切、反余切,反正割,反余割为x的角。
三角函数的反函数是个多值函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数y=x对称。欧拉提出反三角函数的概念,并且首先使用了“arc+函数名”的形式表示反三角函数。
反三角函数的图像与性质