-
-
椭圆面积公式:S=π(圆周率)×a×b,其中a、b分别是椭圆的长半轴,短半轴的长。椭圆面积公式属于几何数学领域。

面积推导导数方法
设椭圆x^2/a^2+y^2/b^2=1
取第一象限内面积有y^2=b^2-b^2/a^2*x^2
即y=√(b^2-b^2/a^2*x^2)
=b/a*√(a^2-x^2)
由于该式反导数为所求面积,观察到原式为圆方程公式*a/b,根据(af(x))'=a*f'(x),且x=a时圆面积为a^2π/4
可得当x=a时,1/4S=b/a*1/4*a^2*π=abπ/4
即S=abπ。
此方法比较容易理解。
椭圆定义
第一定义
平面内与两定点F1、F2的距离的和等于常数2a(2a>▏F1F2▕)的动点P的轨迹叫做椭圆。
即:▏F1▕+▏F2▕=2a
其中两定点F1、F2叫做椭圆的焦点,两焦点的距离▏F1F2▕=2c<2a叫做椭圆的焦距。P为椭圆的动点。
椭圆截与两焦点连线重合的直线所得的弦为长轴,长为2a。
椭圆截垂直平分两焦点连线的直线所得弦为短轴,长为2b。
第二定义
椭圆平面内到定点F(c,0)的距离和到定直线l:x=a2/c(F不在l上)的距离之比为常数c/a(即离心率e,0<e<1)的点的轨迹是椭圆。
其中定点F为椭圆的焦点,定直线L称为椭圆的准线(该定直线的方程是
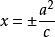
(焦点在x轴上),或
![]()
(焦点在y轴上))。
其他定义
根据椭圆的一条重要性质:椭圆上的点与椭圆长轴(事实上只要是直径都可以)两端点连线的斜率之积是定值,定值为e2-1(前提是长轴平行于x轴。若长轴平行于y轴,比如焦点在y轴上的椭圆,可以得到斜率之积为-a²/b²=1/(e²-1)),可以得出:
在坐标轴内,动点(x,y)到两定点(a,0)(-a,0)的斜率乘积等于常数m(-1<m<0)。
注意:考虑到斜率不存在时不满足乘积为常数,所以x=±a无法取到,即该定义仅为去掉四个点的椭圆。
椭圆也可看做圆按一定方向作压缩或拉伸一定比例所得图形。