-
-
第一个,计算平均值Avg。第二个,计算sigma。第三个,3 sigma = 3* sigma。西格玛是数学中常用的符号的中音音译,是希腊字母∑,英文译音是Sigma, 表示数学中的求和号,主要用于求多项数之和。

sigma的算法
第一个,计算平均值Avg。
Avg = (a0 + a1 + ......+ an-1) / n
第二个,计算sigma。
sigma = sqrt( ( (a0-avg) ^2 + (a1-avg) ^2 + ..... +(an-1 -avg) ^2 ) / (n-1) )
第三个,3 sigma = 3* sigma
6 sigma = 6 * sigma
想要计算一组数据的2sigma,方法如下:
假如有n个数,第一步,先算出样本均值m,如果本身有期望值,则假设m=期望值,如没有期望值,可以用样本均值代替期望值,也就是:
m=(1/n)*(a[1]+a[2]+...+a[n])
第二步,再算样本方差sigma^2,也就是计算样本数据和期望值之间差的平方和。
sigma^2=[1/(n-1)]*{(a[1]-m)^2+(a[2]-m)^2+...+(a[n]-m)^2}
如果有期望值的,上式应是:sigma^2=[1/(n)]*{(a[1]-m)^2+(a[2]-m)^2+...+(a[n]-m)^2}
第三步,把样本方差开根号就能得出样本标准差sigma是多少了。
第四步,把sigma乘以3得出结果就行了。
Sigma指数法一般用于地层压力检测,由意大利AGIP公司提出,应用在不能应用dc指数的碳酸盐岩等非碎屑岩地层。
Sigma指数法是按照对钻井参数的处理方法,来计算地层压力梯度来检测异常高压的一种方法。计算的Sigma值事实上是一种岩石骨架强度参数。地层在正常压实的状况下,岩石强度随深度的加大而增大。如果钻与异常压力地层,岩石强度随孔隙压力的加大而减小。
sigma是什么
例如1+2+3+4+......+100=5050可以写成
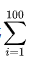
比如下面写i=5,上面写n,后面写xi
表示从x5+x6+…+xn
Sigma(大写Σ,小写σ),是第十八个希腊字母。 在希腊语中,如果一个单字的最末一个字母是小写sigma,要把该字母写成Sigma的小写另一种。在现代的希腊数字代表6。
大写Σ用于:
数学上的总和符号
小写σ用于:
化学上的一种共价键,σ键。
力学上的应力
统计学上的标准差
传热学上的黑体辐射常数
西里尔字母的С及拉丁字母的S都是由Sigma演变而成。