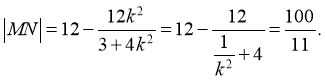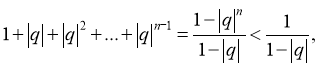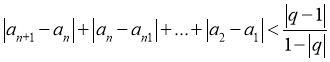-
-
2022湖南高考数学冲刺试卷及答案解析
数学(理工农医类)
一、 选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
A.a>1,b>0 B.a>1,b<0 C. 0<a<1, b>0 D. 0<a<1, b<0
2.对于非0向时a,b,“a//b”的确良 (A)
A.充分不必要条件 B. 必要不充分条件
C.充分必要条件 D. 既不充分也不必要条件
3.将函数y=sinx的图象向左平移![]()
![]() 0
0 ![]()
![]() <2
<2![]()
![]() 的单位后,得到函数y=sin
的单位后,得到函数y=sin![]() 的图象,则
的图象,则![]() 等于 (D)
等于 (D)
 4.如图1,当参数
4.如图1,当参数![]() 时,连续函数
时,连续函数![]() 的图像分别对应曲线
的图像分别对应曲线![]() 和
和![]() , 则 [ B]
, 则 [ B]
5.从10名大学生毕业生中选3个人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数位 [ C]
A 85 B 56 C 49 D 28
6. 已知D是由不等式组![]() ,所确定的平面区域,则圆
,所确定的平面区域,则圆 ![]() 在区域D内
在区域D内
的弧长为 [ B]
7.正方体ABCD—![]()
![]()
![]()
![]() 的棱上到异面直线AB,C
的棱上到异面直线AB,C![]() 的距离相等的点的个数为(C)
的距离相等的点的个数为(C)
A.2 B.3 C. 4 D. 5
A.K的最大值为2 B. K的最小值为2
C.K的最大值为1 D. K的最小值为1 【D】
二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中对应题号后的横线上
9.某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_12__
11、若x∈(0, ![]() )则2tanx+tan(
)则2tanx+tan(![]() -x)的最小值为2
-x)的最小值为2![]() .
.
12、已知以双曲线C的两个焦点及虚轴的两个端点为原点的四边形中,有一个内角为60 ![]() ,则双曲线C的离心率为
,则双曲线C的离心率为![]()
13、一个总体分为A,B两层,其个体数之比为4:1,用分层抽样方法从总体中抽取一个容量为10的样本,已知B层中甲、乙都被抽到的概率为![]() ,则总体中的个数数位 50 。
,则总体中的个数数位 50 。
14、在半径为13的球面上有A , B, C 三点,AB=6,BC=8,CA=10,则
(1)球心到平面ABC的距离为 12 ;
(2)过A,B两点的大圆面为平面ABC所成二面角为(锐角)的正切值为 3
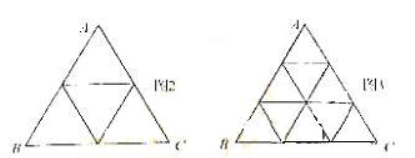
15、将正⊿ABC分割成![]()
![]() (
(![]() ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ![]() ,…,f(n)=
,…,f(n)= ![]() (n+1)(n+2)
(n+1)(n+2)
三.解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
17.(本小题满分12分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的.![]() 、
、![]() 、
、![]() ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。
(I)求他们选择的项目所属类别互不相同的概率;
(II)记![]() 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求
为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求![]() 的分布列及数学期望。
的分布列及数学期望。
解:记第1名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件 ![]() ,
,![]() ,
,![]() ,i=1,2,3.由题意知
,i=1,2,3.由题意知![]()
![]() 相互独立,
相互独立,![]()
![]() 相互独立,
相互独立,![]()
![]() 相互独立,
相互独立,![]() ,
,![]() ,
,![]() (i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(![]() )=,P(
)=,P(![]() )=
)=![]() ,P(
,P(![]() )=
)=![]()
(1) 他们选择的项目所属类别互不相同的概率
(2) 解法1 设3名工人中选择的项目属于民生工程的人数为![]() ,由己已知,
,由己已知,![]() -B(3,
-B(3,![]() ),且
),且![]() =3
=3![]() 。
。
0 | 1 | 2 | 3 | |
P |
解法2 第i名工人选择的项目属于基础工程或产业工程分别为事件![]() ,
,
18.(本小题满分12分)
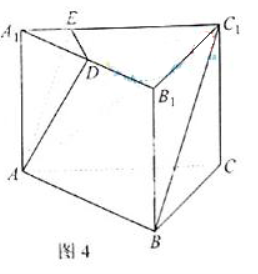
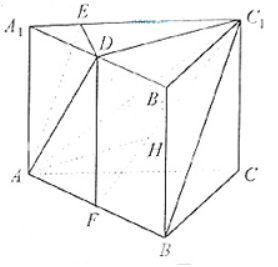
而DE![]() AE。AA
AE。AA![]()
![]() AE=A 所以DE
AE=A 所以DE![]() 平面AC C
平面AC C![]() A
A![]() ,又DE
,又DE![]() 平面ADE,故平面ADE
平面ADE,故平面ADE![]() 平面AC C
平面AC C![]() A
A![]() 。
。
(2)解法1 如图所示,设F使AB的中点,连接DF、DC、CF,由正三棱柱ABC- A![]() B
B![]() C
C![]() 的性质及D是A
的性质及D是A![]() B的中点知A
B的中点知A![]() B
B![]() C
C![]() D, A
D, A![]() B
B![]() DF
DF
由已知AB=![]() A A
A A![]() ,不妨设A A
,不妨设A A![]() =
=![]() ,则AB=2,DF=
,则AB=2,DF=![]() ,D C
,D C![]() =
=![]() ,
,
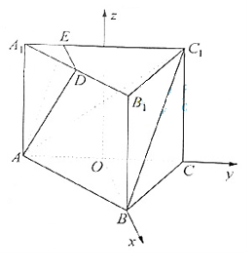
解法2 如图所示,设O使AC的中点,以O为原点建立空间直角坐标系,不妨设
A(0,-1,0), B(![]() ,0,0), C
,0,0), C![]() (0,1,
(0,1,![]() ), D(
), D(![]() ,-
,-![]() ,
,![]() )。
)。
19.(本小题满分13分)
某地建一座桥,两端的桥墩已建好,这两墩相距![]() 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为![]() 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为![]() 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为![]() 万元。
万元。
20(本小题满分13分)
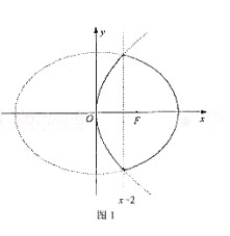
在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标与18之和
(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线I与轨迹C相交于M,N两点,求线段MN长度的最大值。
故点P的轨迹C是椭圆![]() 在直线x=2的右侧部分与抛物线
在直线x=2的右侧部分与抛物线![]() 在直线x=2的左侧部分(包括它与直线x=2的交点)所组成的曲线,参见图1
在直线x=2的左侧部分(包括它与直线x=2的交点)所组成的曲线,参见图1
(i)当k≤![]() ,或k≥
,或k≥![]() ,即k≤-2
,即k≤-2 ![]() 时,直线I与轨迹C的两个交点M(
时,直线I与轨迹C的两个交点M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )都在C
)都在C ![]() 上,此时由④知
上,此时由④知
从而∣MN∣= ∣MF∣+ ∣NF∣= (6 - ![]()
![]() )+ (6 -
)+ (6 - ![]()
![]() )=12 -
)=12 - ![]() (
( ![]() +
+![]() )
)
由 得
得![]() 则
则![]() ,
,![]() 是这个方程的两根,所以
是这个方程的两根,所以![]() +
+![]() =
=![]() *∣MN∣=12 -
*∣MN∣=12 - ![]() (
(![]() +
+![]() )=12 -
)=12 - ![]()
(2)当![]() 时,直线L与轨迹C的两个交点
时,直线L与轨迹C的两个交点![]() 分别在
分别在![]() 上,不妨设点
上,不妨设点![]() 在
在![]() 上,点
上,点![]() 上,则④⑤知,
上,则④⑤知,![]()
21.(本小题满分13分)
(1) 首项为1,公比为![]() 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题
判断所给命题的真假,并证明你的结论;
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题。
判断所给命题的真假,并证明你的结论;
次命题为假命题。
此命题为真命题
本资料由《七彩教育网》www.7caiedu.cn 提供!