2022四川高考数学冲刺试卷

2022四川高考数学冲刺试卷

本试卷分选择题和非选择题两部分。第I卷（选择题）1至2页，第Ⅱ卷（非选择题）3至4页，共4页，满分150分，考试时间120分钟。

注意事项：

1．答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

5．考试结束后，只将答题卡交回。

第I卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设集合，，则 

(A)       (B)      (C)       (D)

2．复数为虚数单位在复平面内对应的点位于

(A)第一象限    (B)第二象限    (C)第三象限    (D)第四象限

3．已知函数，则

(A)    (B)     (C)     (D)

4．为了加强全民爱眼意识，提高民族健康素质，1996年，卫生部，教育部，团中央等12个部委联

合发出通知，将爱眼日活动列为国家节日之一，并确定每年的6月6日为“全国爱眼日”．某校高=(1)班有40名学生，学号为01到40，现采用随机数表法从该班抽取5名学生参加“全国爱眼日’’宣传活动．已知随机数表中第6行至第7行的各数如下：

16 22 77 94 39     49 54 43 54 82   17 37 93 23 78   87 35 20 96 43  84 26 34 91 64

84 42 17 53 31     57 24 55 06 88   77 04 74 47 67   21 76 33 50 25  83 92 12 06 76

若从随机数表第6行第9列的数开始向右读则抽取的第5名学生的学号是

(A)17              (B)23              (C)35              (D)37

5．  ‘‘”是“直线与圆相切”的

(A)充分不必要条件    (B)必要不充分条件   (C)充要条件   (D)既不充分也不必要条件

6．已知离心率为的双曲线，与椭圆有公共焦点，则

双曲线的方程为

(A)(B)(C)(D)

7．执行如图所示的程序框图，则输出的结果为

(A)    (B)    (C)      (D)

8．设函数的导函数是．若，则

(A)    (B)    (C)    (D)

9．如图是某几何体的三视图，若三视图中的圆的半径均为2，则该几何体的表面积为

(A)    (B)    (C)    (D)

10．在平面直角坐标系中，已知直线与曲线为参数

在第一象限恰有两个不同的交点，则实数的取值范围为

(A)(B)(C)(D)

11．已知函数．若，，，则的大小关系为A

(A)    (B)    (C)    (D)

12．设，若关于的不等式在上恒成立，则的最小值是

(A)(B)(C)(D)

第Ⅱ卷（非选择题，共90分）

二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．

13．已知呈线性相关的变量之间的关系如下表：

由表中数据得到的回归直线方程为．则当时，的值为        ．

14．函数的图象在处的切线方程为        ．

15．已知甲，乙，丙三个人中，只有一个人会中国象棋，甲说：“我会”；乙说：“我不会”；丙说：“甲不会”．如果这三句话只有一句是真的，那么甲，乙，丙三个人中会中国象棋的是        ．

16．已知点在椭圆上，是椭圆的左焦点，线段的中点在圆上．记直线的斜率为，若，则椭圆离心率的最小值为        ．

三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17．（本小题满分12分）

2019年12月，《生活垃圾分类标志》新标准发布并正式实施，为进一步普及生活垃圾分类知识，了解居民生活垃圾分类情况，某社区开展了一次关于垃圾分类的问卷调查活动，并对随机抽取的1000人的年龄进行了统计，得到如下的各年龄段频数分布表和各年龄段人数频率分布直方图：

各年龄段频数分布表

(I)请补全各年龄段人数频率分布直方图，并求出各年龄段频数分布表中的值；

(Ⅱ)现从年龄在段中采用分层抽样的方法选取5名代表参加垃圾分类知识交流活动，应社区要求，从被选中的这5名代表中任意选2名作交流发言，求选取的2名发言者中恰有1名年龄在段中的概率．

18．（本小题满分12分）

已知函数在处取得极值，其中．

(I)求的值；

(Ⅱ)当时，求的最大值．

19.（本小题满分12分）

如图①，在菱形中，且，为的中点，将沿折起使，得到如图②所示的四棱锥．

(I)求证：平面平面；

(Ⅱ)若为的中点，求二面角的余弦值．

20.（本小题满分12分）

在同—平面直角坐标系中，圆经过伸缩变换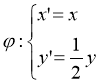后，得到曲线．

(I)求曲线的方程；

(Ⅱ)设直线与曲线相交于两点，连接并延长与曲线相交于点，且．求面积的最大值．

21.（本小题满分12分）

已知函数，．

(I)设的导函数为，试讨论的零点个数；

(Ⅱ)设．当时，若恒成立，求的取值范围．

22.（本小题满分10分）选修4-4:坐标系与参数方程

在平面直角坐标系中，直线的参数方程为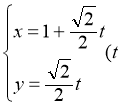为参数．以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

(I)求直线的普通方程和曲线的直角坐标方程；

(Ⅱ)已知点．若直线与曲线相交于两点，求的值．