-
-
2022年天津市高考数学冲刺试卷及答案解析
一、单选题
1.设全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【分析】先计算![]() ,再与集合
,再与集合![]() 进行 交集运算即可求解.
进行 交集运算即可求解.
【详解】因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,
故选:B.
2.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【详解】由![]() ,解得
,解得![]() ,由
,由![]() ,可知“
,可知“![]() ”是“
”是“![]() ”的充分不必要条件,选A.
”的充分不必要条件,选A.
3.函数![]() 的图像大致为
的图像大致为
A.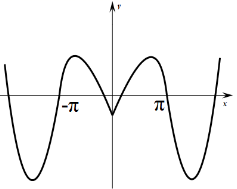 B.
B.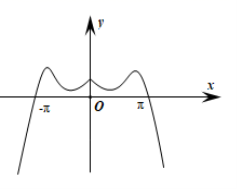
C.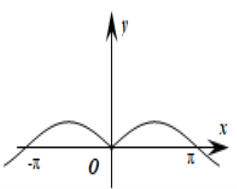 D.
D.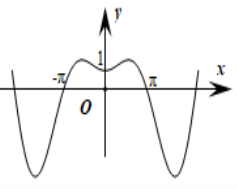
【答案】D
【详解】试题分析:因为![]() ,所以排除A,C,当函数在
,所以排除A,C,当函数在![]() 轴右侧靠近原点的一个较小区间
轴右侧靠近原点的一个较小区间![]() 时,
时,![]() ,函数单调递增,故选D.
,函数单调递增,故选D.
【解析】函数图象与函数性质.
4.对一批产品进行了抽样检测,测量其净重(单位:克),将所得数据分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到如下频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中产品净重落在区间
,并整理得到如下频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中产品净重落在区间![]() 内的个数为( )
内的个数为( )
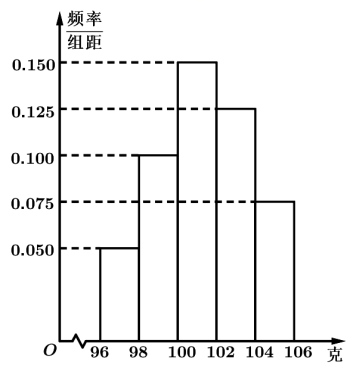
A.90 B.75 C.60 D.45
【答案】A
【分析】根据题意样本中产品净重小于100克的频率为0.3,进而得样本容量为120,再计算样本中产品净重落在区间![]() 内的个数即可.
内的个数即可.
【详解】由题知:样本中产品净重小于100克的频率为![]() ,
,
因为样本中产品净重小于100克的个数是36,
所以样本容量为![]() ,
,
又因为样本中产品净重落在区间![]() 内的频率为
内的频率为![]() ,
,
所以样本中产品净重落在区间![]() 内的个数为
内的个数为![]() .
.
故选:A
5.已知函数![]() ,且
,且![]() ,
,![]() ,
,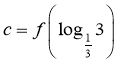 ,则
,则![]() 、
、![]() 、
、![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【分析】先分析![]() 的奇偶性,然后分析
的奇偶性,然后分析![]() 的单调性,再根据自变量的大小以及正负比较出
的单调性,再根据自变量的大小以及正负比较出![]() 的大小关系.
的大小关系.
【详解】因为![]() ,所以定义域为
,所以定义域为![]() 且关于原点对称,
且关于原点对称,
又因为![]() ,所以
,所以![]() 为偶函数;
为偶函数;
当![]() 时,因为
时,因为![]() 、
、![]() 均单调递增,所以
均单调递增,所以![]() 在
在![]() 上也单调递增,
上也单调递增,
又因为![]() ,
,![]() ,
,![]() ,
,
所以 ,所以
,所以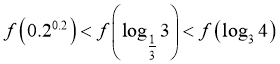 ,所以
,所以![]() ,
,
故选:D.
【点睛】思路点睛:根据函数的性质比较函数值大小关系的一般步骤:
(1)先分析函数的奇偶性,由![]() 以及定义域来确定;
以及定义域来确定;
(2)再分析函数的单调性,由函数解析式或者单调性定义进行判断;
(3)结合奇偶性将待比较的函数值的自变量转换到同一单调区间,再结合单调性即可比较出大小.
6.球与棱长为![]() 的正四面体各条棱都相切,则该球的表面积为( )
的正四面体各条棱都相切,则该球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【分析】采用补形的方法,将正四面体补充为正方体,由此分析出球与正方体的关系,再根据正方体的棱长求解出球的表面积.
【详解】将正四面体补形为一个正方体如图所示(红色线条表示正四面体),则正四面体的棱为正方体的面对角线,
因为球与正四面体的各条棱都相切,所以球与正方体的各个面都相切,所以所求的球为正方体的内切球,
又因为正方体的棱长为![]() ,所以球的半径
,所以球的半径![]() ,
,
所以球的表面积为: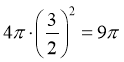 ,
,
故选:C.
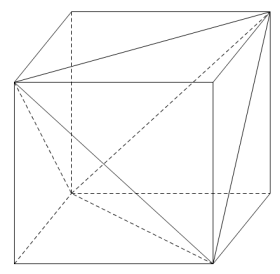
【点睛】关键点点睛:解答本题的关键在于找到正四面体和正方体之间的联系,将原本复杂的正四面体的棱切球问题转化为较为简单的正方体的内切球问题.
7.已知抛物线![]() 上一点
上一点![]() 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线![]() 的左顶点为A且离心率为
的左顶点为A且离心率为![]() ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线![]() 垂直,则双曲线的方程为( )
垂直,则双曲线的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【分析】先求出抛物线的方程,从而得到![]() 的值,根据离心率得到渐近线方程,由渐近线与直线
的值,根据离心率得到渐近线方程,由渐近线与直线![]() 垂直得到
垂直得到![]() 的值,从而可得双曲线的方程.
的值,从而可得双曲线的方程.
【详解】因为![]() 到其焦点的距离为5,故
到其焦点的距离为5,故![]() ,故
,故![]() ,
,
故抛物线的方程为![]() ,故
,故![]() .
.
因为离心率为![]() ,故
,故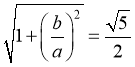 ,故
,故![]() ,
,
根据抛物线和双曲线的对称性,不妨设![]() 在第一象限,则
在第一象限,则![]() ,
,
则![]() 与渐近线
与渐近线![]() 垂直,故
垂直,故![]() ,故
,故![]() ,故
,故![]() ,
,
故双曲线方程为:![]() .
.
故选:D.
【点睛】方法点睛:(1)![]() 上一点
上一点![]() 到其焦点的距离为
到其焦点的距离为![]() ,解题中注意利用这个结论.
,解题中注意利用这个结论.
(2)如果直线![]() 与直线
与直线![]() 垂直,那么
垂直,那么![]() .
.
8.已知函数![]() 的图象与
的图象与![]() 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位,横坐标伸长到原来的2倍得到函数
个单位,横坐标伸长到原来的2倍得到函数![]() 的图象,则下列关于函数
的图象,则下列关于函数![]() 的结论,其中所有正确结论的序号是( )
的结论,其中所有正确结论的序号是( )
①函数![]() 是奇函数
是奇函数
②![]() 的图象关于直线
的图象关于直线![]() 对称
对称
③![]() 在
在![]() 上是增函数
上是增函数
④当![]() 时,函数
时,函数![]() 的值域是
的值域是![]()
A.①③ B.③④ C.② D.②③④
【答案】C
【分析】先根据辅助角公式化简![]() ,然后利用已知条件求解出
,然后利用已知条件求解出![]() 的值,再根据图象的变换求解出
的值,再根据图象的变换求解出![]() 的解析式;①根据
的解析式;①根据![]() 解析式判断奇偶性;②根据
解析式判断奇偶性;②根据![]() 的值判断对称性;③采用整体替换的方法判断单调性;④利用换元法的思想求解出值域.
的值判断对称性;③采用整体替换的方法判断单调性;④利用换元法的思想求解出值域.
【详解】因为![]() ,又
,又![]() 的图象与
的图象与![]() 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为![]() 的等差数列,
的等差数列,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 向左平移
向左平移![]() 个单位得到
个单位得到![]() ,
,
![]() 横坐标伸长到原来
横坐标伸长到原来![]() 倍得到
倍得到![]() ,
,
①![]() 为非奇非偶函数,故错误;
为非奇非偶函数,故错误;
②![]() ,所以
,所以![]() 是
是![]() 的一条对称轴,故正确;
的一条对称轴,故正确;
③因为![]() ,所以
,所以![]() ,
,
又因为![]() 在
在![]() 上先增后减,所以
上先增后减,所以![]() 在
在![]() 上不是增函数,故错误;
上不是增函数,故错误;
④当![]() 时,
时,![]() ,
,
所以![]() ,此时
,此时![]() ;
;![]() ,此时
,此时![]() ,
,
所以![]() 的值域为
的值域为![]() ,故错误;
,故错误;
故选:C.
【点睛】思路点睛:求解形如![]() 的函数在指定区间上的值域或最值的一般步骤如下:
的函数在指定区间上的值域或最值的一般步骤如下:
(1)先确定![]() 这个整体的范围;
这个整体的范围;
(2)分析![]() 在(1)中范围下的取值情况;
在(1)中范围下的取值情况;
(3)根据取值情况确定出值域或最值,并分析对应的![]() 的取值.
的取值.
9.已知函数![]() 对
对![]() ,总有
,总有![]() ,使
,使![]() 成立,则
成立,则![]() 的范围是( )
的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【分析】根据已知条件先分析得到![]() ,然后分析
,然后分析![]() 的几何意义,通过分析
的几何意义,通过分析![]() 与
与![]() 在横坐标相等时,纵坐标竖直距离取最大值的最小值时对应的
在横坐标相等时,纵坐标竖直距离取最大值的最小值时对应的![]() 的取值,由此确定出
的取值,由此确定出![]() 的解析式,同时求解出
的解析式,同时求解出![]() ,由此
,由此![]() 的范围可知.
的范围可知.
【详解】由题意可知:![]() ,
,![]() 成立,即
成立,即![]() ,
,
又对![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() 可看作
可看作![]() 与
与![]() 在横坐标相等时,纵坐标的竖直距离,
在横坐标相等时,纵坐标的竖直距离,
由![]() ,
,![]() ,可取
,可取![]() ,所以
,所以![]() 的直线方程为
的直线方程为![]() ,
,
设![]() 与
与![]() 平行且与
平行且与![]() 相切于
相切于![]() ,所以
,所以![]() ,所以
,所以![]() ,所以切线为
,所以切线为![]() ,
,
当![]() 与
与![]() 平行且与两条直线的距离相等时,即恰好在
平行且与两条直线的距离相等时,即恰好在![]() 的中间,
的中间,
此时![]() 与
与![]() 在纵坐标的竖直距离中取得最大值中的最小值,
在纵坐标的竖直距离中取得最大值中的最小值,
此时![]() ,则
,则![]() ,
,
又因为![]() ,所以
,所以![]() ,所以
,所以![]() ,此时
,此时![]() 或
或![]() 或
或![]() ,
,
所以![]() 的范围是
的范围是![]() ,
,
故选:B.
【点睛】结论点睛:![]() 的几何意义:当
的几何意义:当![]() 与
与![]() 在横坐标相等时,纵坐标的竖直距离.
在横坐标相等时,纵坐标的竖直距离.
二、填空题
10.已知![]() ,i是虚数单位,若(1
,i是虚数单位,若(1![]() i)(1bi)=a,则
i)(1bi)=a,则![]() 的值为_______.
的值为_______.
【答案】2
【详解】试题分析:由![]() ,可得
,可得![]() ,所以
,所以![]() ,
,![]() ,故答案为2.
,故答案为2.
【解析】复数相等
【名师点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如![]()
![]() . 其次要熟悉复数的相关基本概念,如复数
. 其次要熟悉复数的相关基本概念,如复数![]() 的实部为
的实部为![]() 、虚部为
、虚部为![]() 、模为
、模为![]() 、共轭复数为
、共轭复数为![]() .
.
11.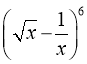 的展开式的常数项为____________.
的展开式的常数项为____________.
【答案】![]()
【详解】试题分析:由题意得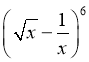 的展开式中的通项为
的展开式中的通项为![]() ,令
,令![]() ,解得
,解得![]() ,所以展开式的常数项为
,所以展开式的常数项为![]() .
.
【解析】二项式定理.
12.设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() __________.
__________.
【答案】![]()
【分析】圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,利用圆的弦长公式,求出
,利用圆的弦长公式,求出![]() 值.
值.
【详解】解:圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,
,
![]() 直线
直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,
![]() 圆心
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
即![]() ,
,![]()
解得:![]() ,
,
解得![]() ,
,
故答案为:![]() .
.
【点睛】本题主要考查直线和圆的位置关系,考查弦长的计算,属于中档题.
13.甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,则一次游戏摸出的白球不少于2个的概率为___________.
【答案】![]()
【分析】根据对立事件的概率公式进行求解即可.
【详解】一次游戏摸出1个白球的概率为:![]() ,
,
一次游戏摸出0个白球的概率为:![]() ,
,
因此一次游戏摸出0个白球或1个白球的概率为:![]() ,
,
所以一次游戏摸出的白球不少于2个的概率为:![]() ,
,
故答案为:![]()
14.已知![]() ,且
,且![]() ,则
,则![]() 的最小值为___________.
的最小值为___________.
【答案】![]()
【分析】由题意可得![]()
![]() ,结合
,结合![]() 和均值不等式可得
和均值不等式可得![]() 的最小值,注意等号成立的条件.
的最小值,注意等号成立的条件.
【详解】由![]() ,且
,且![]() ,可得:
,可得:
![]()
![]() ,
,
结合![]() 可得:
可得:
![]()
![]()
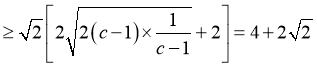 ,
,
当且仅当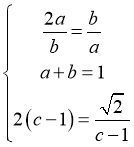 ,即
,即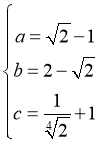 时等号成立.
时等号成立.
【点睛】在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.
15.平行四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 上的动点,
上的动点,![]() ,
,![]() ,则
,则![]() 的最小值为___________.
的最小值为___________.
【答案】![]()
【分析】选取![]() 为基底,由已知计算可得
为基底,由已知计算可得![]() 关系,再设
关系,再设![]() ,
,![]() 可表示为
可表示为![]() 的函数,从而求得最小值.
的函数,从而求得最小值.
【详解】设![]() ,则
,则![]() ,
,![]()
则![]() ,
,![]()
又因为![]() 得
得![]() ,则
,则![]() ,即
,即![]() 得
得![]()
解得![]() ,
,![]() ,
,![]()
设![]()
则![]()
![]()
因为![]() ,所以
,所以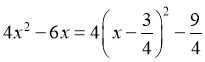
当![]() 时,
时,![]() 取最小值
取最小值![]()
故答案为:![]() .
.
【点睛】关键点点睛:本题解题时选取两个向量为基底,用基底表示所求向量是解题的关键.
三、解答题
16.![]() 的内角
的内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() .已知
.已知![]() .
.
(1)求![]() ;
;
(2)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 及
及![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【分析】(1)先根据正弦定理将原式化简,由此得到![]() 的倍数关系,再结合正弦定理即可得到
的倍数关系,再结合正弦定理即可得到![]() 的值;
的值;
(2)先根据(1)的结果求解出![]() 的值,然后结合两角和的正弦公式和二倍角公式求解出
的值,然后结合两角和的正弦公式和二倍角公式求解出![]() 的值,再根据三角形的面积公式
的值,再根据三角形的面积公式![]() 求解出
求解出![]() 的值,结合余弦定理可求解出
的值,结合余弦定理可求解出![]() 的值.
的值.
【详解】(1)因为![]() ,
,
所以由正弦定理可得![]() ,
,
即![]() ,
,
而![]() ,所以
,所以![]() ,故
,故![]() .
.
(2)由(1)知![]() ,则
,则![]() ,所以
,所以 ,
,
所以![]() ;
;
又![]() 的面积为
的面积为![]() ,则
,则![]() ,
,![]() ,
,
由余弦定理得![]() ,解得
,解得![]() .
.
【点睛】易错点睛:利用正、余弦定理解三角形的注意事项:
(1)注意隐含条件“![]() ”的使用;
”的使用;
(2)利用正弦定理进行边角互化时,要注意结合条件判断将边转化为角的形式还是将角转化为边的形式.
17.如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 是棱PD的中点,且
是棱PD的中点,且![]() ,
,![]() .
.
(I)求证:![]() ; (Ⅱ)求二面角
; (Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 是
是![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 成角的正弦值为
成角的正弦值为![]() ,求
,求![]() 的值.
的值.
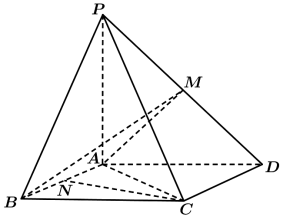
【答案】(I)见解析;(Ⅱ)![]() ;(Ⅲ)1.
;(Ⅲ)1.
【详解】试题分析:(I)![]() ,
,![]() ,所以
,所以![]() 平面PAC;(II)建立空间直角坐标系,求出两个法向量,平面MAB的法向量
平面PAC;(II)建立空间直角坐标系,求出两个法向量,平面MAB的法向量![]() ,
,![]() 是平面ABC的一个法向量,求出二面角;(III)设
是平面ABC的一个法向量,求出二面角;(III)设![]() ,平面MAB的法向量
,平面MAB的法向量![]() ,解得答案.
,解得答案.
试题解析:
证明:(I)连结AC.因为为在![]() 中,
中,

![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
因为AB//CD,所以![]() .
.
又因为![]() 地面ABCD,所以
地面ABCD,所以![]() .因为
.因为![]() ,
,
所以![]() 平面PAC.
平面PAC.
(II)如图建立空间直角坐标系,则![]() .
.
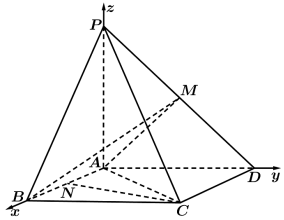
因为M是棱PD的中点,所以![]() .
.
所以![]() ,
,![]() . 设
. 设![]() 为平面MAB的法向量,
为平面MAB的法向量,
所以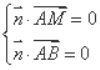 ,即
,即![]() ,令
,令![]() ,则
,则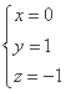 ,
,
所以平面MAB的法向量![]() .因为
.因为![]() 平面ABCD,
平面ABCD,
所以![]() 是平面ABC的一个法向量.
是平面ABC的一个法向量.
所以 .因为二面角
.因为二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的大小为
的大小为![]() .
.
(III)因为N是棱AB上一点,所以设![]() ,
,![]() .
.

设直线CN与平面MAB所成角为![]() ,
,
因为平面MAB的法向量![]() ,
,
所以 .
.
解得![]() ,即
,即![]() ,
,![]() ,所以
,所以![]() .
.
18.椭圆![]() 的离心率
的离心率![]() .
.
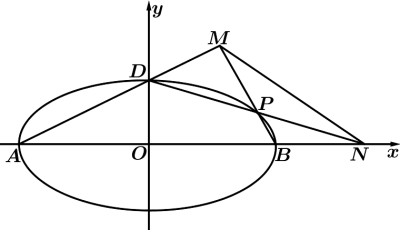
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,![]() 是椭圆
是椭圆![]() 的顶点,
的顶点,![]() 是椭圆
是椭圆![]() 上除顶点外的任意一点,直线
上除顶点外的任意一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,试证明:
,试证明:![]() 为定值.
为定值.
【答案】(1) ![]() +y2=1 (2)见解析
+y2=1 (2)见解析
【详解】(1)![]() ,
,![]()
由(1)知A(-2,0),B(2,0),D(0,1),则直线AD方程为:![]() ;直线BP方程:
;直线BP方程:![]() ,联立得
,联立得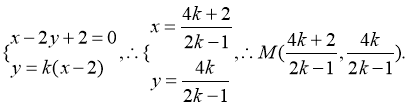 直线BP
直线BP![]() 和椭圆联立方程组解得P点坐标为
和椭圆联立方程组解得P点坐标为![]() ,因为D,N(x,0),P三点共线,所以有:
,因为D,N(x,0),P三点共线,所以有:
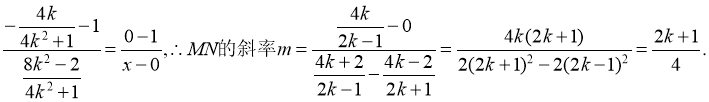
![]()
【解析】本题考查椭圆的标准方程、简单的几何性质,考查直线和椭圆相交问题,定值问题,考查综合解答问题的能力.
19.设![]() 是各项均为正数的等差数列,
是各项均为正数的等差数列,![]() ,
,![]() 是
是![]() 和
和![]() 的等比中项,
的等比中项,![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,使
,使![]() 为整数的
为整数的![]() 称为“优数”,求区间
称为“优数”,求区间![]() 上所有“优数”之和.
上所有“优数”之和.
(3)求![]() .
.
【答案】(1)![]() ,
,![]() ;(2)2036;(3)
;(2)2036;(3)![]() .
.
【分析】(1)根据等比数列的性质列出式子求出![]() 的公差即可得出通项公式;利用
的公差即可得出通项公式;利用![]() 可得
可得![]() 为等比数列,即得通项公式;
为等比数列,即得通项公式;
(2)求出![]() ,可得满足
,可得满足![]() 为整数的
为整数的![]() 形成数列
形成数列![]() ,可得出
,可得出![]() ,求出
,求出![]() 前10项和即可;
前10项和即可;
(3)可得![]() ,则所求即为
,则所求即为![]() 的前n项和,利用错位相减法即可求出.
的前n项和,利用错位相减法即可求出.
【详解】(1)解:设等差数列![]() 的公差为
的公差为![]() ,
,
因为![]() ,
,![]() 是
是![]() 和
和![]() 的等比中项,
的等比中项,
所以![]() ,即
,即![]() ,
,
解得![]() ,因为
,因为![]() 是各项均为正数的等差数列,
是各项均为正数的等差数列,
所以![]() ,故
,故![]() ,
,
因为![]() ,所以
,所以![]() ,
,
两式相减得:![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
![]()
![]() 是以2为首项,2为公比的等比数列,
是以2为首项,2为公比的等比数列,![]()
![]() .
.
(2)![]() ,
,
![]()
![]() ,
,
要使![]() 为整数,则应满足
为整数,则应满足![]() (
(![]() ),
),
即满足![]() 为整数的
为整数的![]() 形成数列
形成数列![]() ,
,
由题可得![]() ,解得
,解得![]() ,
,
则满足条件的“优数”之和为
![]() ;
;
(3)设![]()
![]() ,
,
则![]() 即为数列
即为数列![]() 的前
的前![]() 项和,设为
项和,设为![]() ,
,
则![]() ,
,
∴![]() ,
,
两式相减得:
![]()
∴![]() ,∴
,∴![]() .
.
【点睛】方法点睛:数列求和的常用方法:
(1)对于等差等比数列,利用公式法可直接求解;
(2)对于![]() 结构,其中
结构,其中![]() 是等差数列,
是等差数列,![]() 是等比数列,用错位相减法求和;
是等比数列,用错位相减法求和;
(3)对于![]() 结构,利用分组求和法;
结构,利用分组求和法;
(4)对于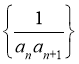 结构,其中
结构,其中![]() 是等差数列,公差为
是等差数列,公差为![]() ,则
,则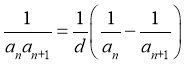 ,利用裂项相消法求和.
,利用裂项相消法求和.
20.已知![]() ,
,
(1)求![]() 在
在![]() 处的切线方程以及
处的切线方程以及![]() 的单调性;
的单调性;
(2)对![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的最大整数解;
的最大整数解;
(3)令![]() ,若
,若![]() 有两个零点分别为
有两个零点分别为![]() ,
,![]()
![]() 且
且![]() 为
为![]() 的唯一的极值点,求证:
的唯一的极值点,求证:![]() .
.
【答案】(1)切线方程为![]() ;单调递减区间为
;单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() (2)
(2)![]() 的最大整数解为
的最大整数解为![]() (3)证明见解析
(3)证明见解析
【分析】(1)求出函数的导数,求出![]() ,
,![]() 即可得到切线方程,解
即可得到切线方程,解![]() 得到单调递增区间,解
得到单调递增区间,解![]() 得到单调递减区间,需注意在定义域范围内;
得到单调递减区间,需注意在定义域范围内;
(2)![]() 等价于
等价于![]() ,求导分析
,求导分析![]() 的单调性,即可求出
的单调性,即可求出![]() 的最大整数解;
的最大整数解;
(3)由![]() ,求出导函数分析其极值点与单调性,构造函数即可证明;
,求出导函数分析其极值点与单调性,构造函数即可证明;
【详解】解:(1)![]()
所以定义域为![]()
![]() ;
;
![]() ;
;![]()
所以切线方程为![]() ;
;
![]() ,
,
令![]() 解得
解得![]()
令![]() 解得
解得![]()
所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)![]() 等价于
等价于![]() ;
;
![]() ,
,
记![]() ,
,![]() ,所以
,所以![]() 为
为![]() 上的递增函数,
上的递增函数,
且![]() ,
,![]() ,所以
,所以![]() ,使得
,使得![]()
即![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
且![]() ;
;
所以![]() 的最大整数解为
的最大整数解为![]() .
.
(3)![]() ,
,![]() 得
得![]() ,
,
当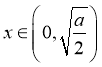 ,
,![]() ,
,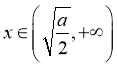 ,
,![]() ;
;
所以![]() 在
在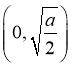 上单调递减,
上单调递减,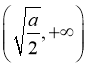 上单调递增,
上单调递增,
而要使![]() 有两个零点,要满足
有两个零点,要满足![]() ,
,
即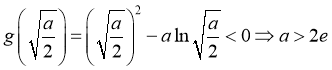 ;
;
因为![]() ,
,![]() ,令
,令![]()
![]() ,
,
由![]() ,
,![]() ,
,
即:![]() ,
,
![]()
而要证![]() ,
,
只需证![]() ,
,
即证:![]()
即:![]() 由
由![]() ,
,![]() 只需证:
只需证:![]() ,
,
令![]() ,则
,则![]()
令![]() ,则
,则![]()
![]()
故![]() 在
在![]() 上递增,
上递增,![]() ;
;
故![]() 在
在![]() 上递增,
上递增,![]() ;
;
![]() .
.
【点睛】本题考查导数的几何意义,利用导数研究函数的极值,最值以及函数的单调性,综合性比较强,属于难题.
欢迎访问“高中试卷网”——http://sj.fjjy.org
·1·