-
-
tanx的导数等于(secx)^2,tanx的二次方再加1等于(secx)^2,(1)sec²x=1+tan²x。(2)secx=1/cosx,cscx=1/sinx,(3)sin²x+cos²x=1,(4)tanx=sinx/cosx。
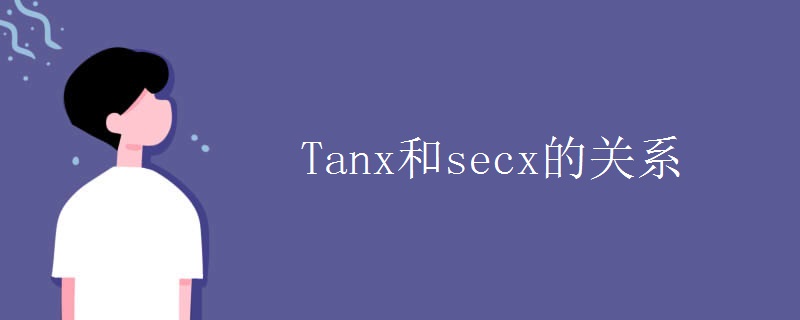
tan²x+1=sec²x。
解答过程如下:
tan²x=sin²x/cos²x。
tan²x+1=sin²x/cos²x+1=sin²x/cos²x+cos²x/cos²x=1/cos²x。
而1/cos²x=sec²x。
正割与余弦互为倒数,余割与正弦互为倒数。
同角三角函数的基本关系式
倒数关系:tanα·cotα=1、sinα·cscα=1、cosα·secα=1;
商的关系:sinα/cosα=tanα=secα/cscα、cosα/sinα=cotα=cscα/secα;
和的关系:sin2α+cos2α=1、1+tan2α=sec2α、1+cot2α=csc2α;
平方关系:sin²α+cos²α=1。