-
-
反比例函数的几何意义为:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数,从而有k的绝对值。

反比例函数的概念
一般地,如果两个变量x、y之间的关系可以表示成y=k/x (k为常数,k≠0)的形式,那么称y是x的反比例函数。因为y=k/x是一个分式,所以自变量X的取值范围是X≠0。而y=k/x有时也被写成xy=k或y=k·x^(-1)。表达式为:x是自变量,y是因变量,y是x的函数。
反比例函数图像的画法
①列表:自变量的取值应以原点为中心,在原点的两侧取三对(或三对以上)互为相反数的值,填写 y值时,只需计算一侧的函数值,另一侧的函数值是与之对应的相反数;
②描点:描出一侧的点后,另一侧可根据中心对称去描点;
③连线:按照从左到右的顺序连接各点并延伸,连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线,注意双曲钱的两个分支是断开的,延伸部分有逐渐靠近坐标轴的趋势,但永远不与坐标轴相交。
反比例函数k值几何意义详解
在 y=k/x(k ≠ 0)这一反比例函数函数当中,要想对系数 k 的几何意义进行全面掌握,就必须掌握以下几点:
第一,应促使学生明确当 y=k/x 这一双曲线距离坐标轴越远时,就会产生越大的 |k| 值;第二,在对一般情况下和
特殊情况下的反比例函数进行分析的过程中,能够对方程所形成的过程产生深刻认知,在此基础上学生才可以灵活
应用反比例函数表达式进行图形面积的计算,在这一过程中,学生可以通过观察图像面积的方式,对反比例函数中 K 值进行确定。
例如,下图例题中“在 y=k/x(k ≠ 0)这一反比例函数函数当中,其中 K 值呈现出重要的几何意义。
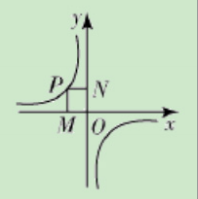
即在 y=k/x 这一反比例函数中取P点(P属于任意一点),假设 PM、PN 分别为 P 与 x 轴和 y 轴之间的垂线,在
此基础上形成的 PMON 这一矩形,以 S=PM·PN=|y|·|x|=|xy|=|k|,将 O、P 相连,得出 S △ POM=S △ PON=k/2”。在
对这一例题进行解答的过程中可以发现,只有对k的几何意义进行灵活应用,才能够更加高效的解决相关反比例函数问题