-
-
李华作为高考英语作文中延续30年的虚拟人物,其存在已成为中国考生的集体记忆符号,但近年来考生对其频繁出现的复杂情绪逐渐显现。“李华”再度现身高考英语作文,考生:不想再帮李华写信。

考生:不想再帮李华写信了怎么回事
一、考生抗拒的根源
角色设定的荒诞性
李华被设定为1977年出生,2025年已48岁,却仍以“高三学生”身份存在,甚至在不同中学频繁转学。这种“永不毕业”的奇幻设定让考生感到脱离现实,戏称“建议他考成人自考”。部分考生认为其“需要代笔写信”的学渣属性与年龄形成强烈反差,质疑角色的可信度。30任务模式的固化与异化
传统代笔式写作(如建议信、邀请函)已被考生视为机械训练,而近年考题中李华的身份扩展至国际倡议者、校报编辑甚至“杠精”,要求考生处理更复杂的现实议题(如联合国青少年倡议、教授分组矛盾),开放性增强的同时也引发“过度介入他人事务”的吐槽。有考生直言:“教授的事你少管!
情感投射的割裂
李华承载着考生对青春的记忆,但长期高频出现导致情感疲劳。内蒙古考生在最后一次模考中用中文写信告别李华,获得满分评价,这种“浪漫告别”成为情感宣泄的出口。广州考生考后喊话“李华肯定考不上大学”,则将应试压力转化为黑色幽默。
二、转型期的集体告别
考生通过多种形式与李华“和解”:
戏谑解构:社交媒体出现“李华虚荣论”(“什么都不会还交外国朋友”)、“相亲需求”(“帮介绍帅哥”)等二次创作,消解严肃性。
仪式化终结:考生在作文结尾添加“Yours sincerely”签名时,将之视为“青春落款”。兰州考生直接宣告“再也不会帮你写信”,完成心理断离。
未来预言:上海交通大学发起“告别李华”活动,暗示高等教育阶段对其使命的终结。而“大学四六级还要写信”的调侃,折射对评价体系连贯性的担忧。
李华的持续存在,既是标准化考试传统的缩影,也是观察教育理念转型的窗口。考生“不想再帮李华写信”的呼声,实质是对评价模式创新、学习自主权提升的期待。这个虚拟人物终将随教育改革渐行渐远,但其承载的集体记忆,仍会在互联网亚文化中持续发酵。
北京高考英语作文题目是什么
假设你是红星中学高三学生李华。联合国正面向全球青少年开展倡议征集活动。你的外国好友Jim打算参加,为此发来邮件,就倡议内容询问你的建议。请你用英文给他回复,内容包括:
1. 提出的建议;
2. 建议的理由。
提示词:倡议 proposal
注意:
1.词数100左右;
2.开头和结尾已给出,不计入总词数。
(网络收集)2025年天津数学高考真题文字版
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]()
A.![]()
B.![]()
C.![]()
D.![]()
2.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的 ( )
”的 ( )
A.充分不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
3. 已知函数![]() 的图象如下,则
的图象如下,则![]() 的解析式可能为 ( )
的解析式可能为 ( )
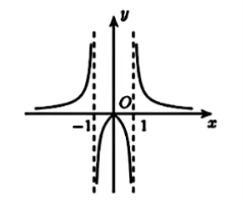
A.![]()
B.![]()
C.![]()
D.![]()
4.若![]() 为直线,
为直线,![]() 为两个平面,则下列结论中正确的是( )
为两个平面,则下列结论中正确的是( )
A.若![]() ,
,![]() ,则
,则![]()
B.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,则
,则![]()
D.若![]() ,
,![]() ,则
,则![]()
5.下列说法中错误的是( )
A.若![]() ,则
,则![]()
B.若![]() ,
,![]() ,则
,则![]()
C.![]() 越接近
越接近![]() ,相关性越强
,相关性越强
D.![]() 越接近
越接近![]() ,相关性越弱
,相关性越弱
6.![]() ,则
,则![]() 的前
的前![]() 项和为( )
项和为( )
A.112
B.48
C.80
D.64
7.函数![]() 的零点所在区间是( )
的零点所在区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
8.![]() ,在
,在![]() 上单调递增,且
上单调递增,且![]() 为它的一条对称轴,
为它的一条对称轴,![]() 是它的一个对称中心,当
是它的一个对称中心,当![]() 时,
时,![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
9.双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,以右焦点
,以右焦点![]() 为焦点的抛物线
为焦点的抛物线![]() 与双曲线在第一象限的交点为
与双曲线在第一象限的交点为![]() ,若
,若![]() ,则双曲线的离心率
,则双曲线的离心率![]() ( )
( )
A.![]()
B.![]()
C.![]()
D.![]()
二、填空题:本大题共6个小题,每小题5分,共30分.
10.已知![]() 是虚数单位,则
是虚数单位,则![]() ______.
______.
11.在![]() 的展开式中,
的展开式中,![]() 项的系数为______.
项的系数为______.
12.![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与圆
,与圆![]() 交于
交于![]() 两点,
两点,![]() ,则
,则![]() ______.
______.
13.小桐操场跑圈,一周2次,一次5圈或6圈。第一次跑5圈或6圈的概率均为0.5,若第一次跑5圈,则第二次跑5圈的概率为0.4,6圈的概率为0.6;若第一次跑6圈,则第二次跑5圈的概率为0.6,4圈的概率为0.4。小桐一周跑11圈的概率为__________;若一周至少跑11圈为运动量达标,则连续跑4周,记合格周数为![]() ,则期望
,则期望![]() __________。
__________。
14.![]() 中,
中,![]() 为
为![]() 边中点,
边中点,![]() ,
,![]() ,
,![]() ,则
,则![]() __________;若
__________;若![]() 且
且![]() ,则
,则![]() __________。
__________。
15.若![]() ,对
,对![]() ,均有
,均有![]() 恒成立,则
恒成立,则![]() 的最小值为__________。
的最小值为__________。
三、解答题:本大题共5小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本题满分14分)
在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() 。已知
。已知![]() ,
,![]() ,
,![]() 。
。
(I)求![]() 的值;
的值;
(II)求![]() 的值;
的值;
(III)求![]() 的值。
的值。
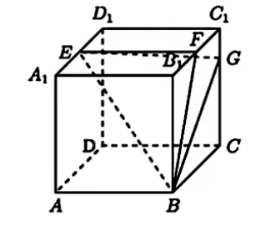
17.(本题满分15分)
正方体![]() 的棱长为4,
的棱长为4,![]() 分别为
分别为![]() 中点,
中点,![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求平面![]() 与平面
与平面![]() 夹角的余弦值;
夹角的余弦值;
(III)求三棱锥![]() 的体积。
的体积。
18.(本题满分15分) 已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,
,![]() 为
为![]() 上一点,且直线
上一点,且直线![]() 的斜率为
的斜率为![]() ,
,![]() 的面积为
的面积为![]() ,离心率为
,离心率为![]() 。 (I)求椭圆的方程; (II)过点
。 (I)求椭圆的方程; (II)过点![]() 的直线与椭圆有唯一交点
的直线与椭圆有唯一交点![]() (异于点
(异于点![]() ),求证:
),求证:![]() 平分
平分![]() 。
。
19.(本题满分15分) ![]() 是等差数列,
是等差数列,![]() 是等比数列,
是等比数列,![]() ,
,![]() ,
,![]() 。 (I)求
。 (I)求![]() ,
,![]() 的通项公式; (II)
的通项公式; (II)![]() 有
有![]() ,
,![]() 。 (i) 求证:
。 (i) 求证:![]() ,均有
,均有![]() ; (ii) 求
; (ii) 求![]() 所有元素之和。
所有元素之和。
20.(本题满分16分) 已知函数![]() 。 (I)
。 (I)![]() 时,求
时,求![]() 在点
在点![]() 处的切线方程; (II)
处的切线方程; (II)![]() 有
有![]() 个零点
个零点![]() ,且
,且![]() 。 (i) 求
。 (i) 求![]() 的取值范围; (ii) 证明:
的取值范围; (ii) 证明:![]() 。
。